728x90
반응형
머신러닝에서 회귀 알고리즘은 가장 기본이면서도 가장 널리 사용되는 모델이다. 이 글에서는 대표적인 회귀 알고리즘 5가지에 대해 개념, 수학식, 실생활 예제, Python 코드, 장단점을 정리한다.

1. K-최근접 이웃 (K-Nearest Neighbors, K-NN)
K-NN은 주변에 있는 K개의 데이터를 찾아 그 평균 또는 다수결로 결과를 예측한다. 직관적인 알고리즘으로, 데이터의 패턴이 명확할 때 효과적이다.
✔️ 수학식
새로운 데이터 xx에 대해, 가장 가까운 KK개의 샘플의 평균으로 예측:

✔️ 실생활 예제
- 추천 시스템: 비슷한 사용자가 좋아한 영화를 추천
- 부동산 가격 예측: 주변 유사 매물 기준 가격 산정
✔️ Python 예제
from sklearn.neighbors import KNeighborsRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
X, y = load_boston(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model = KNeighborsRegressor(n_neighbors=5)
model.fit(X_train, y_train)
print(model.score(X_test, y_test))2. 선형 회귀 (Linear Regression)
입력값과 출력값 사이가 직선 관계일 때 가장 잘 작동하는 기본 회귀 알고리즘이다.
✔️ 수학식
입력 xx와 출력 yy의 선형 관계:

✔️ 실생활 예제
- 광고비와 매출 예측: 광고 지출이 증가할수록 매출이 선형적으로 증가하는 경우
- 시간에 따른 온도 변화: 일정한 경향이 있을 때
✔️ Python 예제
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=1)
X_train, X_test, y_train, y_test = train_test_split(X, y)
model = LinearRegression()
model.fit(X_train, y_train)
print(model.score(X_test, y_test))3. 로지스틱 회귀 (Logistic Regression)
이진 분류 문제에 사용하는 알고리즘으로, 특정 사건이 발생할 확률을 예측한다.
✔️ 수학식
선형 결과를 시그모이드 함수에 넣어 확률로 변환:

결정 기준은 보통 0.5를 기준으로 한다.
✔️ 실생활 예제
- 이메일 스팸 필터링: 스팸일 확률 예측
- 고객 이탈 예측: 이탈 여부를 확률로 판단
✔️ Python 예제
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)
print(model.score(X_test, y_test))4. 다항 회귀 (Polynomial Regression)
데이터가 곡선 형태를 따를 때 사용하는 회귀 방식으로, 비선형 패턴을 설명할 수 있다.
✔️ 수학식
입력 xx에 대해 고차항을 포함한 회귀식:
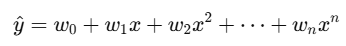
이 수식은 곡선 형태의 데이터를 학습할 수 있게 해준다.
✔️ 실생활 예제
- 자동차 속도와 제동 거리 관계: 제곱에 비례해 증가
- 전력 사용량 예측: 날씨와 사용량 간 비선형 관계
✔️ Python 예제
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
import numpy as np
X = np.arange(10).reshape(-1, 1)
y = X.flatten() ** 2 + 3 * X.flatten() + 5
model = make_pipeline(PolynomialFeatures(degree=2), LinearRegression())
model.fit(X, y)
print(model.predict([[5]]))5. 다중 회귀 (Multiple Linear Regression)
하나의 결과값을 여러 변수로 예측할 때 사용하는 방식이다. 현실 세계의 대부분 문제는 이와 유사하다.
✔️ 수학식

✔️ 실생활 예제
- 집값 예측: 면적, 방 개수, 위치 등 다양한 요인 고려
- 학생 성적 예측: 출석률, 공부 시간, 수면 시간 등
✔️ Python 예제
from sklearn.linear_model import LinearRegression
from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
X, y = load_diabetes(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
model = LinearRegression()
model.fit(X_train, y_train)
print(model.score(X_test, y_test))✅ 알고리즘별 장단점 요약
알고리즘장점단점
| K-NN | 이해 쉬움, 성능 괜찮음 | 속도 느림, 고차원에 약함 |
| 선형 회귀 | 해석 용이, 빠름 | 이상치에 민감, 비선형 관계 처리 못함 |
| 로지스틱 회귀 | 확률 예측, 단순함 | 복잡한 분류에 부적합 |
| 다항 회귀 | 비선형 데이터 대응 | 차수 높으면 과적합 위험 |
| 다중 회귀 | 현실 문제 반영에 적합 | 변수 간 다중공선성 위험 |
마무리
머신러닝 회귀 알고리즘은 각각의 특성에 따라 적절히 적용할 때 큰 효과를 발휘한다. 단순한 분석부터 복잡한 예측까지, 목적에 맞는 알고리즘을 선택하고 실습해보는 것이 중요하다. 위에 소개한 예제 코드를 직접 실행해보면서 차이를 체감해보는 것도 추천한다.
반응형
'IT (IT)🤖🧠 > AI' 카테고리의 다른 글
| 생성형 AI 툴 목적과 사용법 총정리, Midjourney, Runway, Freepik, Adobe Firefly, Lifelike AI, LilysAI 비교 분석 (0) | 2025.04.04 |
|---|---|
| GPT를 개인 비서처럼 활용하는 방법 (뉴스 요약 자동 수신까지 완전 정리) (2) | 2025.04.04 |
| AI로 영상 만들기: 텍스트만으로도 영상 제작하는 방법 정리 (0) | 2025.04.03 |
| AI 부업 - 데이터 라벨링 부업, 자동화로 수익 올리는 실전 꿀팁 (0) | 2025.04.02 |
| AI 부업 - 데이터 라벨링 부업, 어디서 어떻게 시작할까? 국내외 주요 플랫폼 완전 정리 (0) | 2025.04.02 |